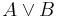Disjunction elimination
| Rules of inference |
|---|
| Propositional calculus |
| Modus ponens Modus tollens Modus ponendo tollens Conjunction introduction Simplification Disjunction introduction Disjunction elimination Disjunctive syllogism Hypothetical syllogism Constructive dilemma Destructive dilemma Biconditional introduction Biconditional elimination |
| Predicate calculus |
| Universal generalization Universal instantiation Existential generalization Existential instantiation |
In propositional logic disjunction elimination, or proof by cases, is the inference that, if "A or B" is true, and A entails C, and B entails C, then we may justifiably infer C. The reasoning is simple: since at least one of the statements A and B is true, and since either of them would be sufficient to entail C, C is certainly true.
For example:
- It is true that either I'm inside or I'm outside. It is also true that if I'm inside, I have my wallet on me. It's also true that if I'm outside, I have my wallet on me. Given these three premises, it follows that I have my wallet on me.
Formally: